Among Us の Discord Overlay タスクするクルー
猫も杓子も Among Us なので Discord StreamKit Overlay Custom CSS Generator for Among Us Streamer 作ったという話.
年末にやっとこさ重い(石によるものではない)腰を上げてSwitchを買ったので配信環境を整えだした.以前WoWsとかちょこちょこやってたときはShadowPlayで録画しておいてストレージがわりにYoutubeに上げては死蔵させていた.で,最近はリモート主体(というかかれこれ1年くらい同僚に顔見せてない)だし,OBSの使い方把握しとくとなんかミーティングとかでも良いことあるのでは?と,Among Usとかイカ2とか雀魂をやったりしながらOBS使ってみてる.映像作りをするアプリだから使用感はお絵描きアプリに近くなるのはまあそうなんだけど出来がよろしくて感心してる.あとMBPは全然OBSでの配信に向いてない.ターミナルとかアプリをフルスクリーンにしてウィンドウキャプチャしてればすぐにどういうことかわかる.デフォのハードウェアエンコーダもちょっと残念な感じだ.
話をやや戻すと自分はぶっちゃけ人狼系があんまり好きじゃなくて,という言い方も違うかな?面白さがよくわからなくてが正しいか,学生の頃人狼BBSが流行ってたあたりで少し触れたくらいで後は雪山の動画見たりとか程度.それでも Among Us はようできてるなーと思う.ゲーム崩壊級のバグとか同期ズレもだいぶあるみたいだけど,なんかこういうのでいいんだよこういうのでって感じがする.クロスプラットフォームでも大して差が出ないくらいマシンパワーいらないし.キャラがカワイイし.
で, Among Us だと発言載せたいからdiscordをoverlayしたいのは当然なんだけど,discordからだとクルーの色がわからないので何色が発言したかわかるようにするにはどこかで紐付けてあげなきゃならない.といっても名寄せできる何かがあるわけでもなく,discordのユーザID拾ってきてDiscord StreamKit Overlayに対するカスタムCSSに埋めるというやりかたがどうも主流みたいなんだけど,ちょっとイイ動きをCSSでさせようとすると何箇所にも同じIDを埋めなきゃならなくなって一々大変になる.凝った見栄えでなくても,プレイヤーではない観戦者がチャンネルに入ってるときにその観戦者はOverlayしたくないとかそれだけでも紐付けに加えて最低2箇所埋めになる.自分がCSS知らんだけで上手いやりようがあるのかもしれないけどちょっと探った感じ特にそういうのもなさそうだった.
なので,まぁ単純作業だし簡単なジェネレータでいいよね.と,Reactどうなってるかなついでに↑のSPA作ってちょっとカワイイ感じの発言アニメーションになるカスタムCSSのクルー色とdiscord IDをシュッと配線できるようにした.これはもう村利あるし白置きしてもろて.
詠唱は不可解だったが、その効力には間違いがなかった。
すっかり年1だけどあんまり長いこと書かないのもアレなのでたまに近況くらいは書いておこうかと
2020年は世の中的にもそうだけど,個人としてもあんまり良い感じではなく総じて謎の石に悩まされる年であった.
昨年末年始あたりからVC6とかいうリファレンスも公開されてない謎な奴のお気持ちをエスパーする作業から始まって,春頃までひととおり足まわりを整備したりしていた.
これにあたりというわけでもないけど「集中し過ぎない/入り込み過ぎないようにする」にはどうするかをちょっと練っていた.というのも,VC4のときちょっと集中し過ぎて*1頚椎をオワらせてしまったことがあったためで,どうも作業内容・量と集中力に対してそれに耐える継戦能力が無いらしい.今年は出社も全くしなくなって雑音や割り込みが入り難くなってしまったのでなおさら意識的に集中し過ぎないための工夫が必要だった.最終的にはVTuberの配信とかをBGMにしておく*2と適度に集中を切ってくれて作業に入り込み過ぎず丁度良い塩梅ということがわかったので今もそんな運用にしてる.通常,技術屋に対しては「どうやって集中するか/集中できる時間を確保するか」が問題になることが多いので,それとある意味逆方向の工夫が必要というのもなんだかなという感じではある.
そんなこんなあってか今回は頚椎等は無事だったのだが,一方で別の問題を錬成してしまったんだよニーサン
ある早朝に激痛で起こされてコイツがもうヤバ.できるだけ近い痛みの表現としては「金的をくらった時の痛みが一瞬で終わらずに継続する」というヤツで吐き気と脂汗が止まらない.救急車召喚ラインか本当に迷ったがその時点まともな判断力があるともわからなかったので,とにかく何かよくわからない対象に謝りながら*3近所の病院が開くまでお布団にくるまってうずくまることになった.その後,採血したりCT撮ったりとかした結果,ローゼンメイデン最凶のドールとして名高い尿結石が左尿管に1つと両腎臓に1つずつ計3つ無償配布されていたことがわかった.勿論ガチャは引けない.特に尿管に投じられた一石が痛みの原因であった.薬も処方されたが「一番の薬は水です.水を飲んで運動して尿管から搾り出して下さい」との解決策を提示され,水はともかくとしてこの激痛下で運動って正気で言ってんのかコイツとか思ったが,痛み止めも処方されたし長男だったので元々してたランニングは継続することにした.次男だったら耐えられなかったかもしれない.別に強くなれる理由はわからなかったがヤバくなったのは確実にOle.それでなんだかんだ血尿が出てたりしたものの今はたまに痛むくらいでそこそこ落ち付いてはいる.が,長いこと膠着状態で石がまだ出てきていないので,腎臓にストックされてるやつが落ちてきたらまた痛むのか?とか,既に尿管にあるやつと玉突き事故が起きたりするのか?とか気にはなる.こぜ1
自分は喉の乾きを感じ難いのかわからないけど元々あまり意識的積極的に水分を取る習慣が無い*4ことが災いしたみたいではある.それでも出社してたらお昼にごはん屋でおひや出てきてそれ飲んでたりはしたけど,リモートになって外食することも無いしそういうきっかけも共に無いなった.今は意識的に水を飲むようにしてはいるが,そうしたいという欲求があるわけでもないし習慣にもなってないので気付いたら飲む程度であり,実際のところどういうペースで飲んだらいいのかよくわかっていない.生活の変化にはそういう落とし穴もあるので他山の石として欲しい.
singletonsの型レベル関数を使ってしまうと示せない性質の例
↓の話
実際singletonsが乱舞するんだけど,singletonsから提供されてる型レベル関数の中には使うと「それ以上証明が進まなくなる」やつが結構な割合で含まれてて,面白味のあるない以前に怒りが先行してしまう.あれは型レベル計算のためのライブラリでしかなくて証明のためのライブラリにはなれてない. https://t.co/ckCcUpWQLK
— Noriyuki OHKAWA (@notogawa) January 3, 2019
サンプルコードはここ
サンプルコードでやろうとしていることは「リストの反転はリスト内要素の置換の一種であることを示す」というもの
まず,2つの型レベルリストが置換の関係にあることを定義する.
data Permutation :: [k] -> [k] -> Type where PermutationNil :: Permutation '[] '[] PermutationSkip :: Sing a -> Permutation xs ys -> Permutation (a : xs) (a : ys) PermutationSwap :: Sing a -> Sing b -> Permutation (a : b : xs) (b : a : xs) PermutationTrans :: Permutation xs ys -> Permutation ys zs -> Permutation xs zs
少しこの定義について確認していく.実際にひとつの例について置換関係にあること確認してみる.
testPermutation :: Permutation [1,2,3,4] [2,4,3,1] testPermutation = PermutationTrans (PermutationSwap s1 s2) $ PermutationTrans (PermutationSkip s2 $ PermutationSwap s1 s3) $ PermutationTrans (PermutationSkip s2 $ PermutationSkip s3 $ PermutationSwap s1 s4) $ PermutationSkip s2 $ PermutationSwap s3 s4
置換は同値関係のひとつなので,反射律,
refl :: Sing xs -> Permutation xs xs refl SNil = PermutationNil refl (SCons x xs) = PermutationSkip x $ refl xs
対称律,
sym :: Permutation xs ys -> Permutation ys xs sym PermutationNil = PermutationNil sym (PermutationSkip s p) = PermutationSkip s $ sym p sym (PermutationSwap a b) = PermutationSwap b a sym (PermutationTrans p1 p2) = PermutationTrans (sym p2) (sym p1)
推移律が示せる.
trans :: Permutation xs ys -> Permutation ys zs -> Permutation xs zs trans = PermutationTrans
先頭への要素の追加と,途中への要素の追加は,置換関係的には同じことを意味する.といった性質も示せる.
here :: Sing a -> Sing xs -> Sing ys -> Permutation (a : xs :++ ys) (xs :++ (a : ys)) here a SNil ys = PermutationSkip a $ refl ys here a (SCons x xs) ys = PermutationTrans (PermutationSwap a x) (PermutationSkip x $ here a xs ys)
さて,反転が置換の一種であること reverseIsPermutation は,
reverseIsPermutation :: Sing xs -> Permutation xs (L.Reverse xs)
のような型をしている.しかし,実際にこれの実装(=証明)を与えようとすると,
reverseIsPermutation SNil = PermutationNil reverseIsPermutation (SCons x xs) = _
までしか進められない.このtyped holeを確認すると,
[-Wtyped-holes]
• Found hole:
_ :: Permutation
(n0 : n1)
(Data.Singletons.Prelude.List.Let6989586621679793554Rev
(n0 : n1) n1 '[n0])となっている.Let6989586621679793554Revって何と,singletonsライブラリのreverseの定義を確認すると,
$(singletonsOnly [d| (snip.) reverse :: [a] -> [a] reverse l = rev l [] where rev :: [a] -> [a] -> [a] rev [] a = a rev (x:xs) a = rev xs (x:a) (snip.) |])
であり,このreverseの定義からTHで生成されるReverseはexportされているが,reverse定義中のwhere節にあるrevはexportされていないので,そこを期待した型が現れてしまうと証明が進められずに止まってしまう.
これはもうどうしようもないので,やるなら自前でreverseを定義して補助関数も参照できるようにしなければならない.
$(singletonsOnly [d| myReverse :: [a] -> [a] myReverse l = myReverseAcc l [] myReverseAcc :: [a] -> [a] -> [a] myReverseAcc [] ys = ys myReverseAcc (x:xs) ys = myReverseAcc xs (x:ys) |])
このmyReverseの定義から生成される MyReverse や MyReverseAcc により,同様に反転が置換であることを示すと
myReverseIsPermutation :: Sing xs -> Permutation xs (MyReverse xs) myReverseIsPermutation xs' = gcastWith (nilIsRightIdentityOfAppend xs') (go xs' SNil) where go :: Sing xs -> Sing ys -> Permutation (xs :++ ys) (MyReverseAcc xs ys) go SNil ys = refl ys go (SCons x xs) ys = PermutationTrans (here x xs ys) (go xs (SCons x ys))
のように示すことができる.nilIsRightIdentityOfAppend は [] がリスト結合演算に対する右単位元であることを示している.
nilIsRightIdentityOfAppend :: Sing xs -> (xs :++ '[]) :~: xs nilIsRightIdentityOfAppend SNil = Refl nilIsRightIdentityOfAppend (SCons _ xs) = gcastWith (nilIsRightIdentityOfAppend xs) Refl
といったように,singletonsのSingの定義は別段問題無いが,Data.Singletons.Prelude 以下のモジュールで定義されている型レベル関数を使ったインターフェースは,それだけで証明ができなくなってしまうようなものが多数存在している.whereやletなどの補助関数により定義されているものは恐らく全滅じゃないだろうか.なので,こういったものをライブラリ外にexportする場合は,そのままsingletonsのものを使うのではなく適宜hideした上で,自分で定義した証明可能なもので代替してexportしたほうが親切じゃないかなと.
cerealのgetFloat*多用はメモリ長者にのみ許されし贅沢
約1年も書いてなかったのか.
ここ2,3年はそこそこのサイズの配列をどうこうする機会が多く,そういうとき特に何も考えなければ Data.Vector に突っ込んでおきたいキモチになる.で,実際に大きな配列をHaskellで扱うとメモリ不足でOOM Killerに殺されたりするわけだけど,そんな原因のひとつについて.
サンプルコードはココにあるのでヒマな人はどうぞ.
stack init stack build
まずputterというexecutableがそこそこ大きな要素数を持ったFloatの配列をlittle endianで出力する.
stack exec putter
これでカレントディレクトリにoutput.dat という50MBくらいのファイルができたかと.次にnaive-getterというexecutableでoutput.datを読み出す.やっていることは,Floatの配列に戻して総和を取り,元の配列の総和と一致するかを見ているだけ.
stack exec naive-getter
naive-getterの実装でByteStringからFloatのVectorに変換する部分は,次の通りcerealでgetFloat32leを使った脳直実装になっている.自然
runGetLazy (V.replicateM len getFloat32le) dat
しかし,コイツが想像以上にメモリをバカ食いするので,適当にプロファイルを見てみる.
stack build --profile stack exec -- naive-getter +RTS -hc -p -s stack exec -- hp2ps -c naive-getter.hp open naive-getter.ps
するとこんな感じになる.すごい.
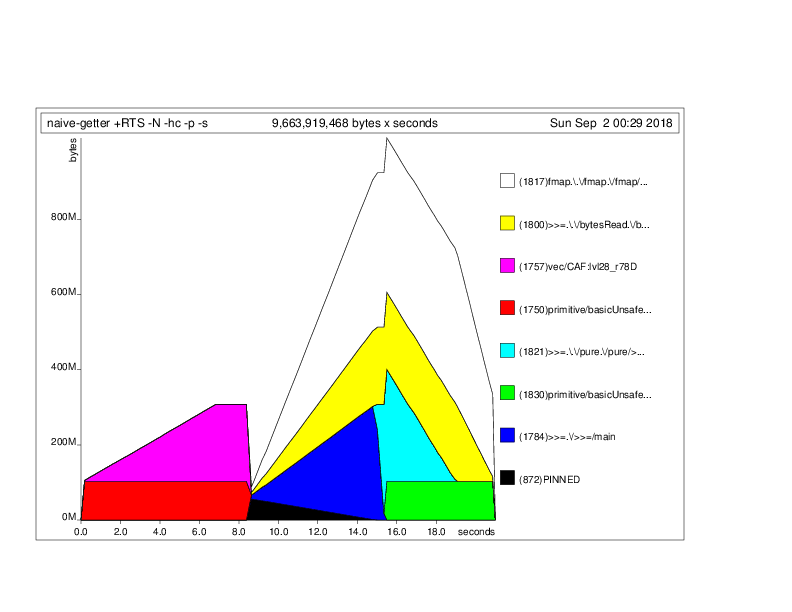
8秒ちょいまではputterが出した配列をgetterでも再度作って総和とか評価してる部分なので無視するとして,Unboxed Vectorではないことを考慮しても以降のメモリ消費は立ち上がり過ぎている.どういうことかとgetFloat32leの実装を見に行くと,次のようになっている.
-- | Read a Float in little endian IEEE-754 format getFloat32le :: Get Float getFloat32le = wordToFloat <$> getWord32le (snip.) {-# INLINE wordToFloat #-} wordToFloat :: Word32 -> Float wordToFloat w = unsafeDupablePerformIO $ alloca $ \(ptr :: Ptr Word32) -> do poke ptr w peek (castPtr ptr)
1要素毎にコレやるわけだが,配列のようなコレクション中の要素を一気にたくさん変換するなら雑に次のような関数でいいかなと別の手段を用意する.
getFloat32leVector :: Int -> Get (V.Vector Float) getFloat32leVector n = do v <- V.replicateM n getWord32le return $ unsafeDupablePerformIO $ alloca $ \ptr -> do V.mapM (\x -> poke ptr x >> peek (castPtr ptr)) v
これでgetFloat32leを置き換えて次のように使ったrevised-getterを作り,
runGetLazy (getFloat32leVector len)
こちらでもnaive-getter同様にprofileを取る.
stack build --profile stack exec -- revised-getter +RTS -hc -p -s stack exec -- hp2ps -c revised-getter.hp open revised-getter.ps
結果はだいぶ減ったことがわかる.それでもまだ大富豪様ではあるわけだが
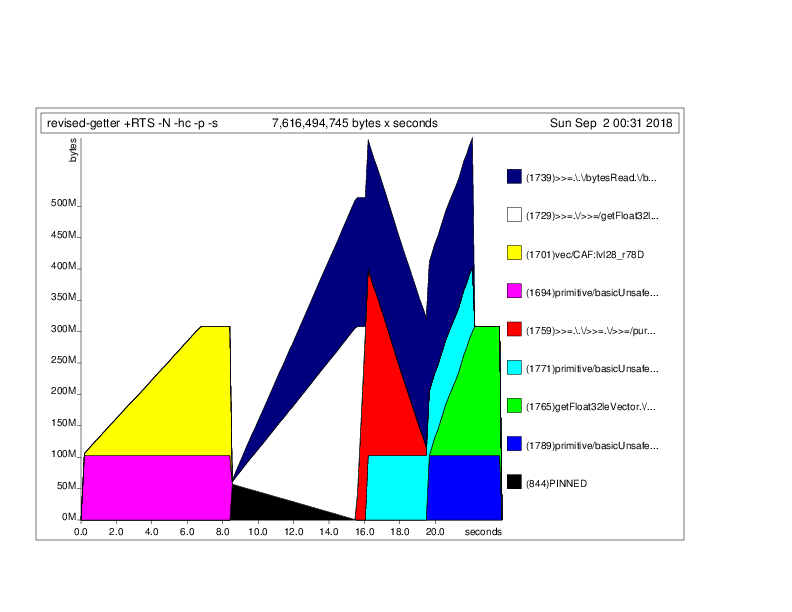
別に総和くらいだったらストリーム処理すばいいんだろうけどそれは簡単のために総和を置いてるだけで,現実的にはもっと配列全体をガチャガチャする処理が控えているためそういうわけにも.
Deep Learning Acceleration勉強会 で発表してきました
Deep Learning Acceleration勉強会 - connpass にてスライドはこちら
www.slideshare.net
普段は出ても関数型言語やら形式手法やらの勉強会とかなため,アウェー感にややソワソワしていた.なんかこの発表で低レイヤマンと思われる可能性があるけどそれでウッカリここに辿り付かれてもスイマセンこのブログの他の記事でもわかるように超高級言語使いですとしか言えない.
思った以上に様々なレイヤーに関する発表がありどこもカリカリにしようとするとガンバリだよねと.そりゃ「計算機科学の全てのレイヤーに精通」とかになっちゃうよなみたいなトコロもこうなってくるとわからんではない.界隈でよくあるやつだとFPGAについての話が無かったので次があるならFPGA勢の進捗は聞いてみたい.
個人的には秋葉さんに「あの記事の者です」と挨拶できたのでよかった.「(ひとつ前の記事)について不快にさせたようで申し訳ない,他のUnagiの方々にもよろしくおねがいします.」と.氏の発表でも自己紹介でKagglerであるというところで「手段を選ばず勝ちにいきます」と言っててここ数日の流れを踏まえてのセリフチョイスしてくれたのかなーと思って面白かった.
既にトゥギャられてるのでこちらも参考
ICFP Programming Contest が本当に縛っていたもの
以前,ここ数年のICFP Programming Contestについて思っていることについてのツイート(群の一部)が, Rustが最強のプログラミング言語である証明 — hayato.io で取り上げらたため, @chokudai さんに届いて反応してくれたようでうれしい.一連の氏のツイートをRTした後,思わず,
ニッコリ
— Noriyuki OHKAWA (@notogawa) 2017年9月1日
一点,ツイッターだと前後の文脈ザックリ落ちることがあるから仕方ないんだけど,正しく伝わってるのか気になったのが,「縛り」の本質について,
そもそも「言語を一つに統一する縛りプレイ」みたいなこと言う人いるけど、各会社さんのプロダクトで使用言語を統一してるものはいくらでもあるわけで。何?そういうの縛りプレイだと思ってるの?と思うし、「超多言語開発でも3日間で形に出来る」ってのを知らしめるのは十分面白いと思うのだけど。
— chokudai(高橋 直大) (@chokudai) 2017年9月1日
あいつは参加するけど推し言語が違うから組めないんだよなーみたいなのがあって自然とチーム人数も絞られてた節もあったと思うんだよね
— Noriyuki OHKAWA (@notogawa) 2017年8月4日
取り上げられたツイートの直後のこのツイートからもわかるように,同僚という固定メンバーとやることが決まってるオシゴトとは異なりチーム組みからできるコンテストでも,推し言語の差を強い制約と認識した場合「いくら強いことがわかってても宗教が違うため組めない奴が出てくる」ことこそがこのコンテストにおける重要な「縛り」であり,何も「言語を一つしか使わないこと」が「縛り」の本質ではないと思っている.
これは,このときの流れの中で @mametter さんとのやりとりでも,
その批判に対しては,選択された1,2言語だけ認定していた時なら「言語が良いからこそ優秀なプログラマを魅了し引き付けたんだ」という反論があったんですが,5~6言語も最強言語に連ねることを許してしまったので反論が使えなくなってしまい,今は正に批判の通りになってると思います.
— Noriyuki OHKAWA (@notogawa) 2017年8月6日
とにかく強い奴で集めたから強いぜ!ということだったら本当にナンデモアリな他のコンテストだろうがそれこそオシゴト・現実世界でもみんなわかっている.
勝ちに行くのもコンテストに参加する上であたりまえのことだし,ルールが何かこの点について縛ってるわけではないのでナンデモアリなコンテストと形式は同じなんだけど,折角 ICFP Programming Contest なら「組めない奴が出てくる」という特徴を愉しめばいいんじゃないかなというのが私見.
まぁ,
残念感はわかるんだけど、むしろ単一の最強言語認定という考え方のほうが現代のプログラミングに即していない、という意見が去年の運営チームで出てたなあ。
— Yusuke Endoh (@mametter) 2017年8月6日
という話もあるので, ICFP Programming Contest も他のコンテストと今はもう何も変わらないのかもしれない.たぶん似たようなことを感じてるのは他にも @shinh さんとかくらいなのかな.
これつまりウナギ批判だと思っていて(他にもあるならすまんすけど)、 https://t.co/VSuSYWkPdv ホントここで書いてたソロ殴りあいやってほしいんだよなあ https://t.co/htHLHiwV8j
— shinichiro hamaji (@shinh) 2017年8月4日
いずれにせよおっさんばかり…なの…では?「組めない奴が出てくる」と思ってたのも思い込みだったのかもしれない.最初から ICFP Programming Contest は言語なんてどうでもよかったのかもしれない.
もちろん禁止ではないわけだし、なんでもあり勢に縛りプレイで勝つってのが最高カッコイイって面もあるから別にどうでもいいんだけど
— Noriyuki OHKAWA (@notogawa) 2017年8月4日
というわけで結論としては最終的にどうでもいい話であるという所に落ち着く.
ただ, @chokudai さんは自らもコンテスト(サイト)を運営する者として,他のコンテスト(だけじゃなく何らかのコミュニティや文化に)乗り込む場合,勝ちだけじゃなくて「それは何を目的にして開催されているのか」についてのこだわりに対し,単に強さを振り回し彼のツイートにある言葉を借りるならば「水差す」ことがないよう多少思いを巡らせて欲しいかなと思う部分もある.自分は彼のつよいぜドヤァみたいなツイートも好きだし実際それ以上につよい.単なる勝ちだけにこだわらず,そういった部分もリスペクトした上でなお勝つ力が彼には十分あると思っている.
一方,彼の場合コンテストで身を立てるのもオシゴトな部分がある.みんながプライベートとして参加するコンテストであっても彼にとっては宣伝・広報を含んだ商業的な意味をメインではないにしろ持たざるを得ないし,周囲もそう捉えると考えるのが自然だろう.彼の事業性質上は強いメンバー集めて勝ってブランディング・アピールするというのはメンバーを集める上でも効果があり正着だ.彼自身がコンテスト強くて成功するモデルケースにならなければならないのだから.だとしたら舐めプにも見えるような甘いムーブをオーディエンスに見せるわけにもいかないだろうし,ましてやそれで負けるのもマイナスではないにしろ機械損失的なものはあるかもしれない.このあたりの立場を考慮すると単にコンテストに参加するだけにしても他の参加者にはない期待を背負っているしリスクを取っている部分があり大変だろうなぁと勝手に心配している.
これからも体に気を付けてがんばって頂きたい.
TensorFlowで訓練したパラメータをChainerのモデルにrestoreする
何がどうなってか深層学習〜的なものに触れる機会が増えたので,何かそれっぽい話を
「他のフレームワークに比べてなんだか学習済み(pre-trained)モデルが公開されてないような?」
Chainerを使ってみた深層学習マンはきっとこのお気持ちになったことがあるんじゃないだろうか.ユーザ数の差だろうか?数は力だよ兄貴!Caffeのモデルファイル(.caffemodel)であれば,ものによってはchainer.links.caffe.CaffeFunctionでロードできるので一応使えはする.global pooling 等で非対応がありロードできないこともあるが,できない部分は飛ばしてロードしてスキマを自分で書いて〜とかできなくはないので,スンナリとロードはできなくともガンバリでロードはできる気がする.
一方,なんだかんだTensorFlowのpre-trainedモデルがckptファイルで公開されていることは多い.
こいつをいざChainerから利用したいとなってもあんまり記事とかが見当たらない.まぁ逆についても無いというか,そもフレームワークを越えてどうにかする話があんまりない.どうにかしたいという雰囲気や動きは散見されるけど,全体からみたらまだ二の次案件のように見える.よく訓練された深層学習マンにはこんなこと呼吸に等しいタスクだからなのか,それともあんまりこういったマネはしないからなのか,もしくは,そんなことせんでも計算資源がありあまってて新規に学習しちゃえばいいだろということなのか.
いずれにせよ,あのモデルをChainerで書いてみたちょっとちゃんと動くか試したい…けど学習済みのものは無くて〜程度のことで,最近あの東京大学でさえ節約していると噂の貴重な貴重な電力(と時間)を消費して新規に学習し始めるというのも心苦しい.Gentoo使いならおさらだ.なので,やっぱりクロスフレームワークでも再利用したいというのはあるんじゃないかなと.
というわけでckptファイル(群)のパラメータをChainerのモデルにrestoreする方法は,
- ckptファイル(pre-trainedなモデル)を入手
- そのckptファイルを学習したTensorFlowのモデルを入手
- TensorFlowのモデルを眺めて各パラメータに付けられた名称を調べる
- TensorFlowのモデルと同じモデルをChainerで書く
- TensorFlowのCheckpointReaderでckptファイルを開く
- ckptファイルから各名称のパラメータを引っ張り出す
- TensorFlowとChainerではweightのdimの順番が違うので必要に応じて転置
- chainer.Linkの対応するパラメータに代入していく
みたいな流れになる.
class CKPT: def __init__(self, path): # ckptファイルを開く self.ckpt = tf.train.NewCheckpointReader(path) # ndim見て決め打ってるけど,そのパラが何のものかはモデルからわかってるので, # 本当は個別にget_conv2d_weightとかget_fc_weightとかを用意したほうがいい def get(self, name): arr = self.ckpt.get_tensor(name) nd = np.ndim(arr) # 必要に応じて転置 if nd == 4: # おそらく 2D Convolution だろうと return arr.transpose(3,2,0,1).copy() # TensorFlow -> Chainer if nd == 2: # おそらく Fully Connected だろうと return arr.transpose(1,0).copy() # TensorFlow -> Chainer if nd == 1: # biasやBatchNormのパラメータだろうと return arr else: pass # unknown weight type # TODO: raise Exception (snip.) # Chainer版のモデル class YourModel(chainer.Chain): def __init__(self): super(YourModel, self).__init__( c0 = L.Convolution2D(3 , 16, 7, 3, 3, nobias=True), bn = L.BatchNormalization(16, 0.9997, 0.001) c1 = L.Convolution2D(None, 32, 3, 1, 1), (snip.) ) def __call__(self, x): (snip.) def restore_from_ckpt(self, path): ckpt = CKPT(path) # 各名称のパラメータを引っ張り出す self.c0.W.data = ckpt.get('PreTrainedModel/Conv2d_0/weights') self.bn.beta.data = ckpt.get('PreTrainedModel/BatchNorm/beta') self.bn.gamma.data = ckpt.get('PreTrainedModel/BatchNorm/gamma') self.bn.avg_mean.data = ckpt.get('PreTrainedModel/BatchNorm/moving_mean') self.bn.avg_var.data = ckpt.get('PreTrainedModel/BatchNorm/moving_variance') self.c1.W.data = ckpt.get('PreTrainedModel/Conv2d_1/weights') self.c1.b.data = ckpt.get('PreTrainedModel/Conv2d_1/bias') (snip.) if __name__ == '__main__': model = YourModel() model.restore_from_ckpt('pre-trained.ckpt') (snip.)
もちろん,これで万事うまくいくというわけではないだろうが.
名前調べるのめんどくさいなぁという場合,CheckpointReaderのget_variable_to_shape_mapでshapeと共に一覧できるので,それ見て判断とかでもできなくはないこともある.